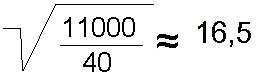ՆերածությունԼույսի ինտերֆերենցի և դիֆրակցիայի երևույթները ցույց են տալիս, որ լույսը տարածվում է ալիքային տեսության օրենքների համաձայն: Այս օրենքների միջոցով մենք կարող ենք լուծել թե համասեռ միջավայրում և թե ցանկացած օպտիկական սիստեմների միջով լույսի տարածման վերաբերյալ խնդիրները, այսինքն` այս կամ այն մակերևութներով և դիաֆրագմաներով սահմանափակված, տարբեր միջավայրերի միակցության միջով լույսի տարածման վերաբերյալ խնդիրները: Սակայն կարևոր գործնական նշանակություն ունեցող հարցերի մի շատ մեծ շրջանում, մասնավորապես, լույսի փնջի ձևավորման (լուսատեխնիկա) հարցերում և պատկերներ առաջանալու (օպտատեխնիկա) հարցերում, երկրաչափական օպտիկայի պատկերացումների օգնությամբ լուծումը կարելի է ստանալ շատ ավելի պարզ ճանապարհով: Երկրաչափական օպտիկան գործ ունի բեկման և անդրադարձման հայտնի օրենքներին ենթարկվող և իրարից անկախ առանձին լուսային ճառագայթի գաղափարների հետ:Լուսային ճառագայթի գաղափարը կարելի է ստանալ դիտարկելով ռեալ լուսային փունջը. որից անցքով ու նեղ դիաֆրագմաների միջոցով մենք առանձնացնում ենք նեղ և զուգահեռ փունջ: Որքան այդ անցքի տրամագիծը փոքր լինի, այնքան առանձնացրած փունջը նեղ կստացվի, և սահմանում, անցնելով ցանկացած չափով նեղ անցքերի, մենք կարող ենք հուսալ ստանալու լուսային ճառագայթը որպես երկրաչափական գիծ: Սակայն մենք գիտենք, որ դիֆրակցիայի երևույթի հեևանքով, նեղ փնջի (ճառագայթի) ցանկացած չափով առանձնացման նման պրոցեսը. անհնարին է: D տրամագծովդիաֆրագմայի միջով անցկացրած լուսային փունջի անխուսափելի լայնացումը որոշվում է 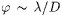 կարգի դիֆրակցիայի անկյունով (1-ին մինիմումի ուղղությունը): Միայն սահմանային դեպքում, երբ λ=O, կստանանք, որ նման լայնացում տեղի չի ունենում, և միայն այդ դեպքում մենք կարող ենք խոսել ճառագայթի մասին որպես երկրաչափական գծի, որի ուղղությունը որոշում է լուսային էներգիայի տարածման ուղղությունը: Այսպիսով, լուսային ճառագայթը աբստրակտ մաթեմատիկական գաղափար է և ոչ թե ֆիզիկական կերպար, և երկրաչափական օպտիկան ռեալ ալիքային օպտիկայի այն սահմանային դեպքն է միայն, որը համապատասխանում է չքացող փոքր լուսային ալիքի երկարությունը: կարգի դիֆրակցիայի անկյունով (1-ին մինիմումի ուղղությունը): Միայն սահմանային դեպքում, երբ λ=O, կստանանք, որ նման լայնացում տեղի չի ունենում, և միայն այդ դեպքում մենք կարող ենք խոսել ճառագայթի մասին որպես երկրաչափական գծի, որի ուղղությունը որոշում է լուսային էներգիայի տարածման ուղղությունը: Այսպիսով, լուսային ճառագայթը աբստրակտ մաթեմատիկական գաղափար է և ոչ թե ֆիզիկական կերպար, և երկրաչափական օպտիկան ռեալ ալիքային օպտիկայի այն սահմանային դեպքն է միայն, որը համապատասխանում է չքացող փոքր լուսային ալիքի երկարությունը: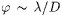 առնչությունը ցույց է տալիս, որ եթե էկրանի կամ անցքի D չափը λ ալիքի երկարության համեմատությամբ մեծ է, ապա համասեռ միջավայրում լույսի ուղղագիծ տարածվելը խախտող անկյունային շեղումը կարող է շատ փոքր լինել: Ուստի ռեալ օպտիկայում, որտեղ λ-ն վերջավոր մեծություն է, երկրաչափական օպտիկայի օրենքներից շեղումները այնքան ավելի քիչ պետք է լինեն, որքան մեծ է D-ի չափը: Դրան համապատասխան սովորական փորձերում մենք դիտում ենք, որ երբ լուսավորում ենք մեծ չափերի մարմինները, ապա կտրուկ ստվերներ են առաջանում: Սակայն առանց դժվարության կարելի է ցույց տալ, որ դիֆրակցիոն շեղումը այս դեպքերում ևս գոյություն ունի: Եթե առարկայից R հեռավորության վրա գտնվող էկրանի վրա ստվեր գցենք, ապա դիֆրակցիոն շերտերի գծային չափերը կունենան ≈αR=λ/D ∙ R արժեքները և, ուրեմն, մեծ R-ի դեպքում կարող են դիտվել,նույնիսկ, եթե անգամ առնչությունը ցույց է տալիս, որ եթե էկրանի կամ անցքի D չափը λ ալիքի երկարության համեմատությամբ մեծ է, ապա համասեռ միջավայրում լույսի ուղղագիծ տարածվելը խախտող անկյունային շեղումը կարող է շատ փոքր լինել: Ուստի ռեալ օպտիկայում, որտեղ λ-ն վերջավոր մեծություն է, երկրաչափական օպտիկայի օրենքներից շեղումները այնքան ավելի քիչ պետք է լինեն, որքան մեծ է D-ի չափը: Դրան համապատասխան սովորական փորձերում մենք դիտում ենք, որ երբ լուսավորում ենք մեծ չափերի մարմինները, ապա կտրուկ ստվերներ են առաջանում: Սակայն առանց դժվարության կարելի է ցույց տալ, որ դիֆրակցիոն շեղումը այս դեպքերում ևս գոյություն ունի: Եթե առարկայից R հեռավորության վրա գտնվող էկրանի վրա ստվեր գցենք, ապա դիֆրակցիոն շերտերի գծային չափերը կունենան ≈αR=λ/D ∙ R արժեքները և, ուրեմն, մեծ R-ի դեպքում կարող են դիտվել,նույնիսկ, եթե անգամ 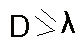 : :
Դժվար չէ հասկանալ, որ օբյեկտների երկու սիստեմները (անցքերի և էկրանների) կտան լրիվ նույնանման դիֆրակցիոն պատկերներ, եթե լույսի աղբյուրի և դիտողի աչքի դասավորությունը և անցքերի ու էկրանների չափերն այնպիսիք են, որ երկու օբյեկտներին էլ համապատասխանում է ֆրենելյան գոտիների և նրանց մասերի միևնույն թիվը: Իրոք, դիֆրակցիոն պատկերի բնույթը որոշվում է հենց ֆրենելյան զոնաների թվով, այլ ոչ թե էկրանների ու անցքերի բացարձակ չափերով:Հարթ ալիքի դեպքում (անսահման հեռացված աղբյուր) ֆրենելյան գոտու մակերեսը հավասար է 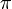 fλ-ի, որտեղ f-ը հեռավորությունն է մինչև դիտողի աչքը, իսկ զոնայիշառավիղը` fλ-ի, որտեղ f-ը հեռավորությունն է մինչև դիտողի աչքը, իսկ զոնայիշառավիղը` 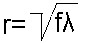 : :Այսպիսով, որպեսզի գոտիների թիվը իրար հավասար լինեն, f հեռավորությունը, x մեծության անցքի դեպքում, պետք է այնպես ընտրել, որ 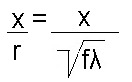 մեծությունն ունենա միևնույն արժեքը: Այսպիսինն է դիֆրակցիոն պատկերների նմանությանպայմանը: Ինչպես երևում է մեծությունն ունենա միևնույն արժեքը: Այսպիսինն է դիֆրակցիոն պատկերների նմանությանպայմանը: Ինչպես երևում է 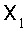 և և 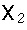 չափի երկու նման օբյեկտների դեպքում, միատեսակ դիֆրակցիոն պատկեր կարելի կլինի դիտել, եթե չափի երկու նման օբյեկտների դեպքում, միատեսակ դիֆրակցիոն պատկեր կարելի կլինի դիտել, եթե 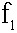 և և 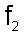 հեռավորությունները մինչև դիտողի տեղը, ընտրված լինեն այնպես, որ հեռավորությունները մինչև դիտողի տեղը, ընտրված լինեն այնպես, որ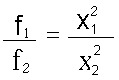 : :
Այսպես, Վ. Կ. Արկադևի փորձերում մոդելների վրա դիֆրակցիոն պատկերը հնարավոր էր իրականացնել ափսե բռնող ձեռքից 11 կիլոմետրով հեռացրած էկրանի վրա. դա հեշտությամբ իրականացվում է 40 մետր հեռավորությունից ձեռքը և ափսեն փոխարինելով թիթեղից կտրած 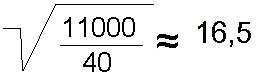 անգամ փոքրացրած մասշտաբի մոդելով: անգամ փոքրացրած մասշտաբի մոդելով:Օգտվելով ճառագայթային օպտիկայի օրենքներից չի կարելի մոռանալ, որ դրանք իրականության միայն առաջին մոտեցումն են, և որ լույսի տարածման և ոչ մի դեպք չի կատարվում առանց դիֆրակցիոն երևույթների: Հետևաբար, պետք է հասկանալ այդ ճառագայթային (երկրաչափական) կառուցումների ալիքային (դիֆրակցիոն) իմաստը: Համապատասխանորեն պարզ է դառնում, որ ճառագայթային օպտիկայի օրենքները սահմանափակ կիրառություն ունեն և պետք է կարողանալ կողմնորոշվել, թե որ պայմաններում այդ օրենքների կիրառությունը թույլատրելի է և գործնականում փորձի հետ համապատասխանության մեջ է գտնվում: Ըստ որում, ստացվում է, որ նույնիսկ գործնական օպտիկայում ամենանուրբ հարցերը (օրինակ` օպտիկական գործիքների լուծիչ ուժի հարցը) լուծվում են դիֆրակցիայի տեսության միջոցով: |
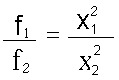 :
: